Coalescence
coalescence of 1 cP salt water drops in a 0.8 cP silicone oil bath, filmed at 16,000 fps
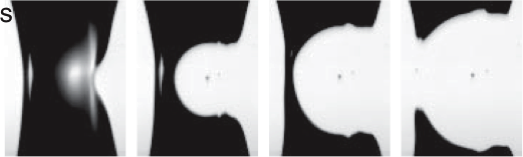
When fluid drops merge, a dramatic transformation occurs: the topology changes as the fluid masses, originally separated, merge into a single entity. At first, the drops are separated by only a small distance. Then a thin fluid bridge is formed between them which rapidly widens due to surface tension forces as shown in the figure. We have employed an electrical method and high-speed imaging to study the coalescence of two drops over a wide range of time-scales and fluid viscosities. We have shown that at low approach velocity, where the drops coalesce as undeformed hemispheres, the viscous-to-inertial crossover is unexpectedly late and inconsistent with the theory. We have presented a new picture of the flow field near the singularity based on an unappreciated length-scale, and it correctly predicts the late crossover. Recently, in collaboration with Osman Basaran's group at Purdue University, we have identified a new regime in coalescence that dominates the asymptotic dynamics of coalescence for drops of any finite viscosity.
See the video abstract on YoduTube.
“Coalescence of bubbles and drops in an outer fluid.” Joseph D. Paulsen, Rémi Carmigniani, Anerudh Kannan, Justin C. Burton, and Sidney R. Nagel, Nat. Commun. 5:3182 doi: 10.1038/ncomms4182 (2014).
“Approach and coalescence of liquid drops in air.” Joseph D. Paulsen, Phys. Rev. E 88, 063010 (2013).
“The inexorable resistance of inertia determines the initial regime of drop coalescence”, J.D. Paulsen, J.C. Burton, S.R. Nagel, S. Appathurai, M.T. Harris, and O.A. Basaran, PNAS 109, 6859 (2012)
“Viscous to Inertial Crossover in Liquid Drop Coalescence”, J.D. Paulsen, J.C. Burton, S.R. Nagel, Phys. Rev. Lett. 106, 114501 (2011).
“Coalescence of low-viscosity fluids in air,” S.C. Case, Phy. Rev. E, 79, 026307, 1-10 (2009).
“Coalescence in low-viscosity liquids,” S. C. Case and S. R. Nagel, Phys. Rev. Lett. 100, 084503 1-4 (2008).
Publications:
Pinchoff
asymmetric air bubble pinch-off in water, filmed at 67,000 fps
A drop falling from a faucet is a common example of a liquid fissioning into two or more pieces. The cascade of structure that is produced in this process is of uncommon beauty. As the drop falls, a long neck, connecting two masses of fluid, stretches out and then breaks. What is the shape of the drop at the instant of breaking apart? Something dire must happen to the mathematical description of the liquid at that point since the drop undergoes a topological transition where it starts out as a single, connected fluid and ends up in two or more separate pieces. This is an example of a finite-time singularity since the drop breakup occurs a short time after the drop becomes unstable and starts to fall. Using photographic techniques, we have been studying transitions such as these to understand how the non-linearities in the governing equations (in this case the Navier-Stokes equations) can be tamed and understood. Singularities of this kind occur in many areas of physics from stellar structure to turbulence to bacterial colony growth. This drop breakup problem is one of the simplest places to start an experiment that directly probes the singularity itself. In collaboration with Wendy Zhang, we have uncovered a variety of different singularities - some of which surprisingly retain a memory of their initial conditions throughout the entire breakup process.
Publications:
“Vibration and Nonlinear Resonance in the Break-up of an Underwater Bubble,” L. Lai, N. Keim, F. Kamel, W. W. Zhang, S. R. Nagel submitted (2013). arXiv:1307.6420
“Perturbed breakup of gas bubbles in water: Memory, gas flow, and coalescence”, N.C. Keim, Phys. Rev. E 83, 056325 (2011).
“Memory-encoding vibrations in a disconnecting air bubble”, L. Schmidt, N.C. Keim, W.W. Zhang, and S.R. Nagel, Nature Physics, DOI: 10.1038/NPHYS1233, (2009).
“Breakup of Air Bubbles in Water: Breakdown of Cylindrical Symmetry,” N. C. Keim, P. Møller, W. W. Zhang, and S. R. Nagel, Phys. Rev. Lett. 97, 144503 (2006).